The Visum fare model is based on fare systems and ticket types.
A fare system is a set of lines, for which a joint fare system exists. Each PuT operator often has his own fare system, in transport associations a fare system can also include lines of different operators.
A ticket type describes how the fare is calculated for a PuT connection or part of a connection. Each ticket type uses one of the following calculation methods ("Fare structure"):
- Distance fare: The fare is conform with the distance covered, which is measured by fare points.
- Zone-based fare: The fare is conform with the number of traversed fare zones.
- From-to zone-based fare: The fare is only dependent on initial fare zone and target fare zone, this is therefore a matrix fare.
- Short-distance fare: A special fare for paths, which do not exceed the specified threshold regarding distance, run time and/or the number of stops.
- Time fare: this fare is based on the journey time.
- Direct distance fare: The price depends on the direct distance between start and end stop point.
The fare structures are described in detail as follows (Base fare calculation).
The Illustration 205 offers an overview of the network objects which belong to the fare modeling in Visum.
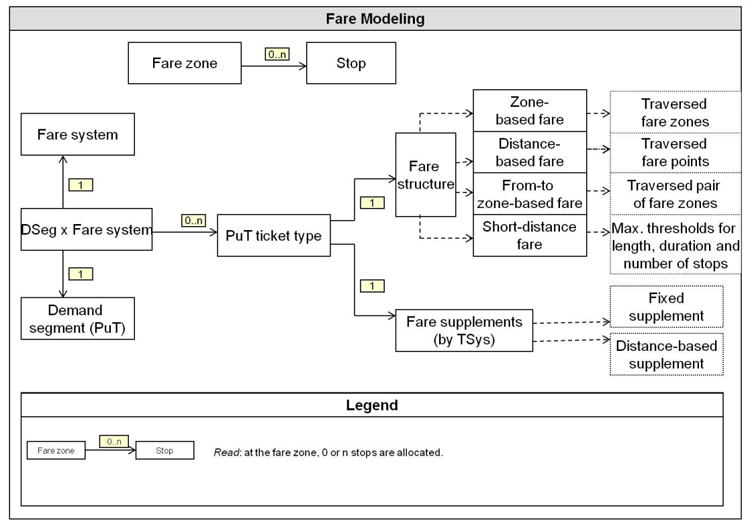
Illustration 205: Possibilities of fare modeling in Visum
For each demand segment you can determine which ticket types are used in a fare system. In particular for each demand segment, several ticket types may exist for each fare system.
With the allocation of lines (and PuT-Aux transport systems) to fare systems, each path leg of a PuT connection belongs to one or more fare systems.
Fare systems are generally independent. The total fare for a connection is normally the sum of the fares to be paid for the individual fare systems. With specific transfer fares you can however model, that a change between fare systems costs extra or a reduction is given (Transport system-specific supplements).
Determining the ticket to be used for each fare system
Within the fare systems, the possibilities of fare modeling are very versatile.
A basic property of a fare system is the "Fare-reference". This expresses, whether a ticket has to be bought for each individual path leg or if it can be used for successive or even all path legs of a connection. All three cases are more often found in practice.
As mentioned, several ticket types (per demand segment) may be available within a fare system. Let's take for example, a fare system is composed of fare zones and the normal fare depends on the number of traversing fare zones. For trips of maximum ten minutes, an inexpensive short-distance ticket applies independent of the fare zones. For trips from and to the airport, a special airport ticket has to be bought.
Generally speaking the crucial question is when creating a fare system, which ticket types are allowed to be used for which connections and how much freedom does the passenger have when selecting a ticket.
The applicability of the different ticket types plays an important role. If the defined conditions in the ticket type have been breached, the ticket cannot be used and another ticket has to be used. In the example, the short-distance ticket is invalid if the maximum run time of 10 minutes has been exceeded and the airport ticket only applies for paths from and to the airport. Distance-, time- or zone-based ticket types can be modeled so that they are only valid on certain connections. You can thus define where the applicability limits of the ticket lie.
Ticket types have ranks, which can be used to express a hierarchical order within a fare system. In combination with the previously described applicability of tickets, a logic thus applies for determining tickets to be used, for a given connection or its path leg(s): Amongst all applicable ticket types it is the one with the highest rank.
In the example shown, the special airport ticket must have the highest rank, because it has to be used for all connections, whose start or target is the airport. For all other connections the airport ticket cannot be used after construction, which is why the ticket type with the second highest rank is regarded, in this case the short-distance ticket. This applies if the connection fulfills the requirements of a short-distance ticket. If this is not the case, the normal zone-based fare with the lowest rank is applied.
Do you want to illustrate that the passenger has the free choice between several ticket types, then allocate the same rank. The most inexpensive ticket with the highest rank is selected amongst all applicable tickets.
Ranking order of fare systems
It may occur, that lines do not just belong to one fare system, but are part of several fare systems. A regional train can for example, be used both within the urban network area with a network ticket and beyond the boundaries of the transport association with a long-distance ticket. Urban network and long-distance transport are separate fare systems with completely different fare structures, the regional train line however, belongs to both.
If a line belongs to several fare systems, a fare within each of these fare systems can generally be determined according to the procedure described above. However, in reality the passenger cannot freely select between the two different fare systems, in each case. A typical fare condition would be, for example, that the regional train on trips within the transport association area can only be used with ticket types of the urban network fare system and long-distance transport tickets only have validity if used beyond the transport association boundary (Procedure for ambiguous fare systems).
To express such ranking, you can define fare system ranks. These ranks are only relevant if in your network model, lines belong to several fare systems, because otherwise the fare systems are evident for all path legs of a PuT connection.
In general the line of each path leg of a PuT connection belongs to several fare systems. A set of allocated fare systems therefore exists for each path leg. The entire connection can principally be "covered" by any combination of items of these fare system sets. The fare system ranks then define a logical order within the combinations: all combinations with the smallest maximal fare system rank are considered first, and thus the one selected which can be applied and provides the lowest fare. If none is applicable, all other combinations with the next highest rank follow. If there are no valid fare system combinations, the global fall-back fare of the fare model is charged.
Because you can allocate ranks both on the ticket type level and the fare system level to model specific fare conditions, all together great flexibility is achieved for fare modeling.
|
Note: In the directory C:\Users\Public\Documents\PTV Vision\PTV Visum 2024/Examples, you can find examples of use on this topic. The PuT Ticket Fares Timetable shows the modeling of a fare model as well as various ticket types in combination with the timetable-based PuT assignment. The PuT Ticket Fares Headway example describes the possibilities of fare modeling using fare points. |